优化是深度学习中的关键组成部分。在深度模型中，我们通常需要设计一个模型的损失函数来约束训练过程，并朝着最小化代价函数的方向去训练。然而，由于深度网络的复杂性，使得深度学习中的优化问题面临着诸多困难和挑战，至今仍未得到一个完美的解决方案。目前，深度神经网络的参数学习主要是通过梯度下降法来寻找一组可以最小化结构风险的参数。本文从梯度下降法出发，通过探寻深度优化问题中的若干可改进点，对优化算法的变体进行归类探究。除此之外，文章还简要分析了模型的初始化参数和输入值尺度这两个重要方面，辅助优化算法在深度模型上获得更好的效果。

优化算法是深度学习中十分重要的环节。深度学习中的优化，往往是通过给定一个以模型参数为变量的函数，一般称为损失函数或目标函数，通过具体算法找到合适的参数值，使得该函数最小化[17]。从理论上来说，对于一个存在解析形式的函数，一定能够通过最优性条件[1;13]求解出显式最优解。然而，由于方程求解的难度过大，往往使用基于迭代的数值计算方法去优化目标。较为常见的有梯度下降法、牛顿法、共轭梯度法等。

摒弃了传统机器学习对于人工特征工程的高度依赖，深度学习往往通过构建复杂度高、参数量大的深层次网络模型，去让模型自主学习到繁杂的数据特征。但是，面对如此高复杂度的含参模型，算力的限制对模型的训练速度提出了很高的要求。同时，高维度的损失函数存在着大量不可预知的特殊因素，例如函数中的鞍点、高原、平坦区域等，这些对优化算法的性能也提出了很高的要求。因此，相较于传统的机器学习优化算法[19;2]，必须在它们的基础上做出相应的改进，以解决它们被应用在深度学习中时面临的诸多困境。

本文从最传统的一阶和二阶优化算法出发，首先在第 2 节介绍了经典的梯度下降法和牛顿法，为后续的变体算法做铺垫。之后三个章节从三个视角切入，对优化算法的改进版本进行了分类和对比。第 3 节从训练速度和精度的角度出发，探究了在训练过程中，每次训练时输入数据的规模大小对优化问题的影响。第 4 节探究了收敛速度对整个训练过程的影响，通过改进学习率设置来让收敛速度自适应整个训练过程，保证收敛的准确性。第 5 节考虑到随机梯度下降中梯度估计的随机性，故对梯度估计方法进行了修改，使梯度更新在训练过程中更加稳定。最后，第 6 节放眼优化算法之外，探究了模型初始化参数和输入值尺度两大重要因素对优化准确度的影响，并给出了已有的一些解决方案。全文的工作流程以及对优化问题的划分如图 1 所示。

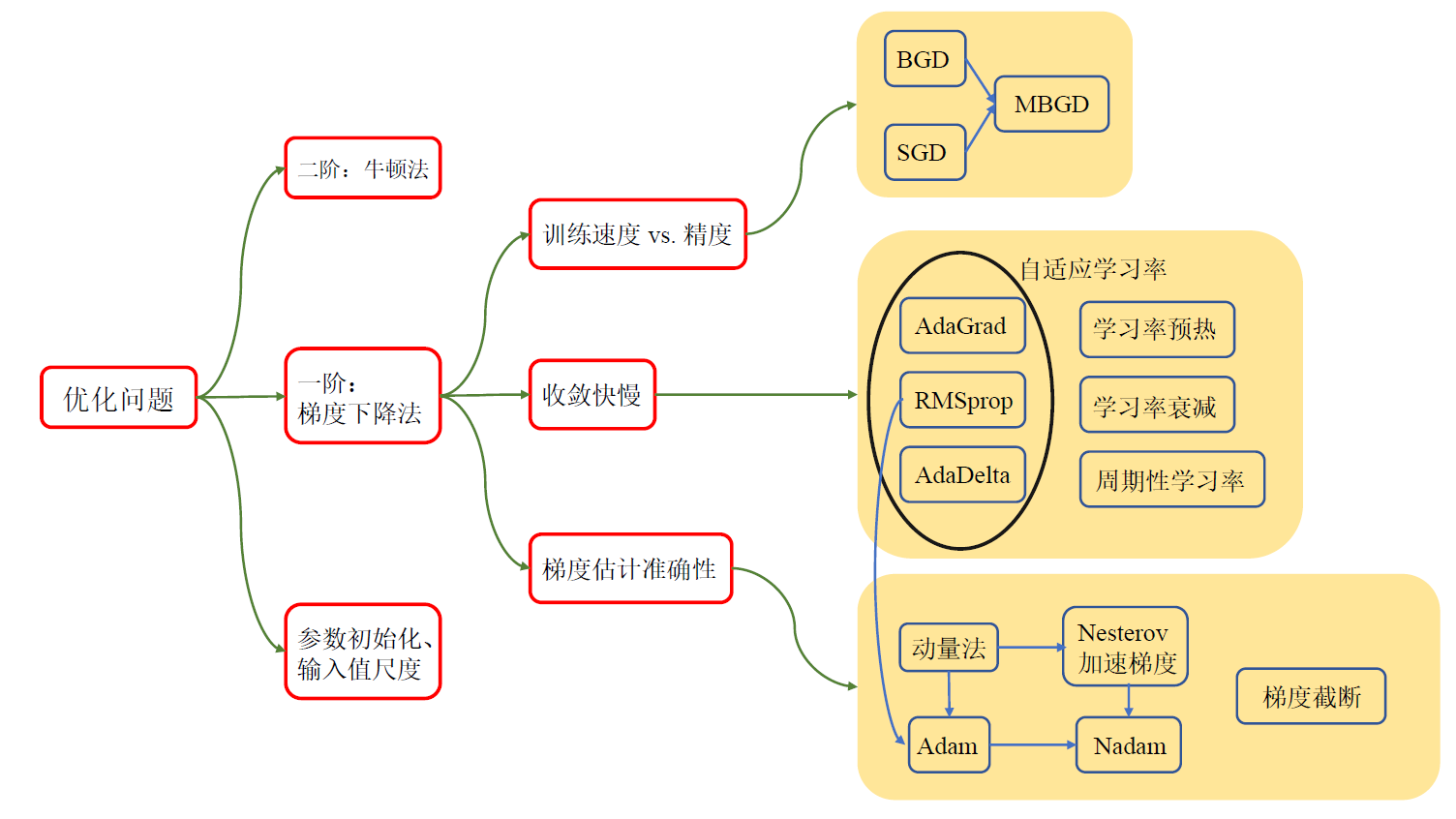
以有监督模型为例，我们首先对优化问题的定义进行简单的描述。假设输入数据$(x_i, y_i) \in \mathbb{R}^{d_x} imes \mathbb{R}^{d_y}$，$i=1,2,…,n$，其中$n$为输入的样本数量。对于具体任务而言，我们需要学习一个网络映射，将输入值$x_i$映射为一个新的取值$\hat{y}_i$，作为该网络的输出值，即模型的预测值。之后，将预测值$\hat{y}_i$与真实值$y_i$进行对比，该过程一般通过构造损失函数来实现，该函数往往反映了真实值和预测值之间的误差大小。优化算法所需要解决的，便是最小化该损失函数这一重要问题。

我们首先构造一个网络映射 $f_{ heta} : \mathbb{R}^{d_x} imes \mathbb{R}^{d_y}$，其中 $ heta$ 为需要优化的网络参数集合。同时，定义损失函数为 $\mathcal{L}(\cdot, \cdot)$，则优化问题可被形式化定义为

$$
\min_{ heta} \frac{1}{n} \sum_{i=1}^n \mathcal{L} (y_i, f_{ heta}(x_i))
$$

损失函数的选取对于优化问题也十分关键，通常来说，我们需要根据具体任务的需求来设置特定于任务的损失函数。例如，对于回归预测问题，我们通常采用均方误差损失函数，即 $\mathcal{L}(y, y’)=||y - y’||^2$。对于分类问题，我们通常采用交叉熵或KL散度来比较预测分布和真实分布之间的差异。

本部分我们将介绍深度学习优化问题中的两大基础算法 —— 梯度下降法和牛顿法，分别对应基本的一阶和二阶算法。后续针对优化算法的改进，通常在这两个基础算法上进行迭代更新。

2.2.1 梯度下降法

梯度下降法是一种基于迭代的最小化目标函数的优化算法。对于函数 $f(x)$， 若 $f(x)$ 在 $x$ 附近连续可微，则 $f(x)$ 下降最快的方向为 $f(x)$ 在 $x$ 点处的梯度反方向。基于这一思想，假设目标函数为 $J( heta)$ ，其中 $ heta$ 为模型参数，则梯度下降法需要利用该函数的反向梯度 $- abla_{ heta} J( heta)$，来对目标参数进行更新。同时，该方法还设置了一个学习率 $\alpha$，来进一步限制每次更新时的步长大小。

具体的，假设参数 $ heta$ 的初始值为 $ heta_0$，则对于第 $t$ 次参数更新，迭代公式为

$$
heta_{t+1}= heta_t - \alpha abla_{ heta} J( heta)
$$

通过迭代更新，将会生成参数序列 $ heta_0. heta_1, heta_2, …， heta_t, …$，直至该序列收敛到期望最优解 $ heta^*$，则算法终止。
该算法由于利用了目标函数的一阶导数进行迭代更新，故被归为一阶优化算法。

2.2.2 牛顿法

牛顿法[3]是一种基于二阶导数的迭代优化算法。对于目标函数 $J( heta)$，假设 $J( heta)$ 连续二阶可微，将其在 $ heta_t$ 处进行二阶泰勒展开，并取二阶近似

$$
J( heta) \approx J( heta_t) + abla_{ heta} J( heta_t)^T ( heta - heta_t) + \frac{1}{2} ( heta - heta_t)^T abla^2_{ heta} J( heta_t)( heta - heta_t)
$$

其中，$ abla^2_{ heta} J( heta_t)$ 是 $J( heta)$ 在 $ heta_t$ 处的 Hesse 矩阵。令 $ abla_{ heta} J( heta)=0$，则

$$
abla_{ heta} J( heta_t) + abla^2_{ heta} J( heta_t)( heta - heta_t)=0
$$

设 $ abla^2_{ heta} J( heta_t)$ 可逆，则可以得到牛顿法的迭代公式

$$
heta_{t+1}= heta_t - abla^2_{ heta} J( heta_t)^{-1} abla_{ heta} J( heta_t)
$$

相比于基于一阶导数的梯度下降法，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑走了一步之后，坡度是否会变得更大。因此，牛顿法比梯度下降法看得更远一点，能更快地走到最底部。而梯度下降法每次只从当前所处位置选一个坡度最大的方向走一步。可视化效果如图 2 所示。

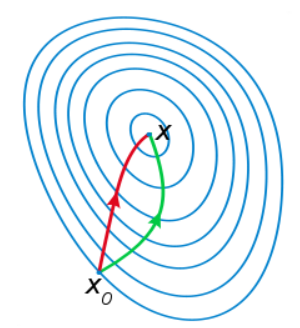
尽管牛顿法收敛更快，但是每次迭代的时间比梯度下降法长，因此相对而言并不常用。接下来介绍的所有优化算法，均在一阶梯度下降法的基础上进行改进。

深度学习中，为了减少单次训练时的随机性影响，避免因为数据噪声产生的不收敛现象，而引入了“批处理”的思想。简而言之，就是在单次训练过程中，向网络中传入多组数据，数据规模称为 batch size，一次完整的训练称为一个 batch。对于一个batch中的每个训练样本，我们都会得到一个单独的损失值，通过对所有样本的损失值取平均，构造最终的损失函数，来减弱单样本的随机性误差。然而，随着batch size的增大，每次训练需要的样本数增多，所耗费的时间代价也会随之增加。因此，需要在精度和速度之间，找寻到一个微妙的平衡。

本部分将以 batch size 为分类依据，介绍三种典型算法。首先介绍随机梯度下降（SGD）和批量梯度下降（BGD），分别对应速度和精度的两个极端情形。最后在此基础上引入小批量梯度下降（MSGD），通过调整控制 batch size的大小，来平衡精度和速度两项指标之间的关系。

对于每一次参数更新，最朴素的思想则是将所有训练样本放入网络，利用完整的数据集进行损失函数的计算。这种思想的主要依据在于，利用全数据集训练时，确定的梯度下降方向能够更好地代表样本总体，从而能够更加准确地朝向极值方向。

假设数据集规模为 $n$，输入样本为 $(x^{(i)}, y^{(i)})$，$i=1,2,…,n$，则 $t+1$ 时刻的迭代公式为

$$
heta_{t+1}= heta_t - \alpha \cdot \frac{1}{n} \sum_{i=1}^n abla_{ heta} J( heta; x^{(i)}; y^{(i)})
$$

大规模样本下，模型收敛的稳定性得到了保证。同时，由于batch size较大，所需要的batch数随之减少，因此总的训练时间会进一步缩短。然而，过大的 batch size ，使得模型的探索性变差，容易在起始点附近很近的地方停止更新。同时，样本中的噪声影响显著削弱，使得函数难以跳出尖锐极小点[9]，从而限制了模型的泛化能力。

随机梯度下降[16]处理了 batch size 大小为 1 时的情形，即每次进行参数更新时，只使用一个训练样本。假设输入为 $x^{(i)}$，对应标签为 $y^{(i)}$，则迭代公式为

$$
heta_{t+1}= heta_t - \alpha \cdot abla_{ heta} J( heta; x^{(i)}; y^{(i)})
$$

相比于全批量梯度下降法，随机梯度下降的一大优势在于，由于每次训练样本的随机性，使得样本中的噪声也能够被充分利用，进而提升了模型的泛化能力。同时，由于每次训练时只需要考虑唯一的样本，因此训练速度也会显著增加，可以被用作在线学习。
然而，该方法的缺点也十分明显。由于噪声的增多，尽管模型的泛化能力增强，但也增加了模型的收敛难度。尽管每次迭代整体上会朝着最优方向下降，但每次更新时的方向较为杂乱，且容易陷入局部极小值或鞍点。

在 BGD 和 SGD 中，我们发现，batch size的大小对优化算法的结果，会产生较为显著的影响，且主要集中在“精度”和“速度”这两个重要维度。在 BGD 中，我们使用了全数据集样本进行单次训练。尽管样本数的扩大，会使得模型收敛更加稳定，但单次训练需要遍历完整的数据集，使得训练速度大大降低。在 SGD 中，我们使用了随机的单一样本进行单次训练。由于每次只需计算一个样本，因此单次训练的速度大大提高，但噪声的影响在训练过程中被显著放大，对于模型的收敛准度带来了极大的挑战。

MSGD 方法的引入，正是为了解决batch size 过大或过小，而导致的精度和速度无法收敛的问题。假设每一次训练中使用 $m$ 个样本，则 $t+1$ 时刻的迭代公式为

$$
heta_{t+1}= heta_t - \alpha \cdot \frac{1}{m} \sum_{i=1}^m abla_{ heta} J( heta; x^{(i)}; y^{(i)})
$$

一般来说，$m$ 的取值在几到几百之间，可以根据具体任务规模而定。batch size的变动可以随之对学习率的大小进行调整。batch size设置较大时，随机梯度方差越小，则训练更稳定，可以设置更大的学习率。batch size 较小时，需要较小的学习率来保证收敛稳定。对于batch size和学习率之间的调整关系，我们可以采用线性缩放原则来进行大致估计，即批量大小增加 $k$ 倍时，学习率也增加 $k$ 倍。

小批量梯度下降已经称为了梯度下降法中的一个最优变体模型。然而，该算法仍然存在着若干挑战。首先，batch size 作为一个重要的超参数，需要我们根据具体训练效果进行人工调整。其次，学习率设置和梯度估计方法这两部分，在迭代公式中也是不可被忽视的因素。因此，我们需要对这两部分进行进一步的优化，使得 MSGD 方法能够获得更好的性能。

在前一部分中，所有的参数迭代公式均包含一项超参数，即学习率 $\alpha$，用来控制参数在更新迭代时的步幅大小。学习率的选取对于参数的更新至关重要，它决定了网络模型是否能够收敛至全局最小值。若学习率过大，则模型难以收敛，若学习率过小，则模型收敛过慢，如图 3 所示。因此，我们需要在梯度下降法的基础上，对训练过程中的学习率进行优化调整，使得模型的收敛过程更加符合预期效果。

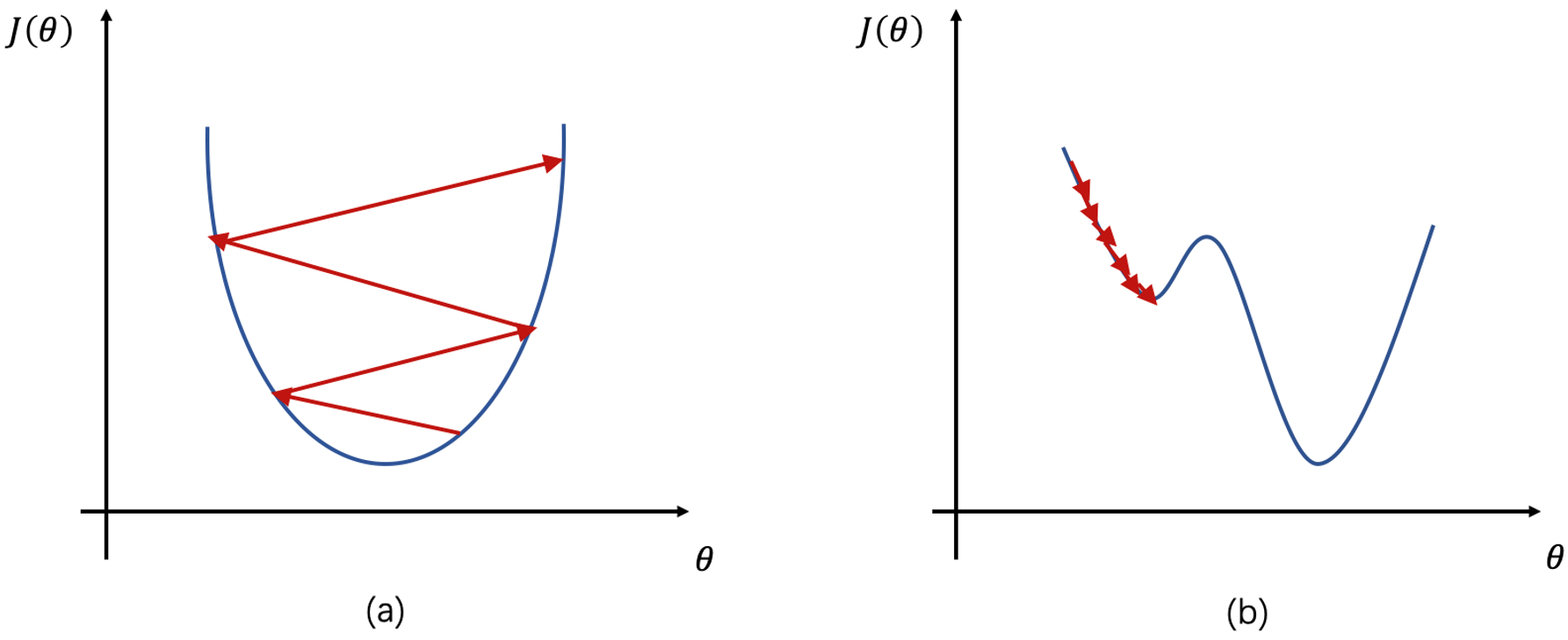
由于刚开始训练时,模型的参数是随机初始化的，此时若选择一个较大的学习率,可能会使得模型不稳定，产生振荡现象。因此，通过预热学习率的方式，可以使得训练初期的学习率较小,在小学习率下，模型可以慢慢趋于稳定。等模型相对稳定后，再去选择预先设置的学习率进行训练,使得模型收敛速度变得更快，模型效果更佳。

假设预热的迭代总次数为 $T$，初始学习率为 $\alpha_0$，当前迭代次数为 $t$，则最初的 $T$ 次迭代中，学习率动态变化的计算方式为

$$
\alpha_t=\alpha_0 \cdot \frac{t}{T}
$$

一般来说，在参数更新初期，由于距离最优点较远，因此应该保证较大的学习率，充分探索邻近区域，保证较快的收敛速度。到达后期时，参数逐步逼近最优点，因此需要保证较小的学习率，来防止在最优点附近来回震荡。

基于这样的经验，我们发现，随着参数更新的不断进行，需要不断降低学习率的数值，使得更新的步幅逐渐变小，保证收敛的稳定性。从这点出发，我们可以通过将学习率常量改变为一个随时间动态可变的数值，来满足这一要求。

不失一般性，我们将学习率按迭代次数 $t$ 进行衰减。设学习率初始值为 $\alpha_0$，在 $t$ 次迭代时的学习率为 $\alpha_t$，则可给出 $\alpha_t$ 关于迭代次数和学习率初始值的衰减函数表达式 $\alpha_t=f(\alpha_0, t)$。常见的衰减表达式有如下几种：

• 阶梯衰减： 该方法每经过 $T_1, T_2, …, T_m$ 次迭代，将学习率衰减为原来的 $\beta_1, \beta_2, …, \beta_m$ 倍，所有参数均为人工设置的超参数。
• 指数衰减： 设 $\beta < 1$ 为衰减率，则 $\alpha_t=\alpha_0 \beta^t$，$\beta$ 可取0.95，0.98等。
• 自然指数衰减： 设 $\beta$ 为衰减率，则 $\alpha_t=\alpha_0 e^{-\beta imes t}$，$\beta$ 可取0.02，0.05等。
• 逆时衰减： 设 $\beta$ 为衰减率，则 $\alpha_t=\alpha_0 \frac{1}{1 + \beta imes t}$。
• 余弦衰减： 设 $T$ 为总的迭代次数，则 $\alpha_t=\frac{1}{2} \alpha_0 (1 + \cos (\frac{t \pi}{T}))$。

对于一个完整的训练过程，通常结合使用预热和衰减两种学习率调整方式。训练开始时，由于参数初始化的随机性，需要将学习率控制在一个较小的范围，逐渐增大，直至训练稳定。稳定后，模型的分布就较为固定了，若还沿用较大的学习率，就会破坏稳定性，很有可能错过局部最优点。这时应逐步降低学习率，使得模型能够稳定收敛至局部最小值。

通过学习率预热和衰减的方式，收敛稳定性的问题已经可以被初步解决。然而，在参数迭代的过程中，函数鞍点和尖锐最小值的存在，使得模型参数极有可能陷入较差的局部最优解。因此，考虑到这些特殊情况的存在，我们需要适当的对学习率进行增大，使得参数能够有更大概率逃离尖锐或平坦最小值。尽管这样的操作，在短期内可能损害优化过程，但从长远来看，有助于找到更优的局部最小值[7]。

周期性学习率[12;18]调整方法是在保证模型收敛稳定的基础上，对函数中的特殊点进行了一个更为周到的考虑，使其能够跳出较差的局部最优，向着更优的局部最小去探索。常用的周期学习率调整方法有如下两种：

• 循环学习率： 让学习率在某个区间内周期性增大或减小。假设一个循环周期为 $2 \Delta T$，其中前 $\Delta T$ 步线性增大，后 $\Delta T$ 步线性减小。假设循环周期数为 $m$，则第 $t$ 次迭代时，所在的循环周期数 $m$ 为
  $$
  m=[1 + \frac{t}{2\Delta T}]
  $$

假设第 $m$ 个周期内，学习率最大和最小值分别为 $\alpha_{\min}^m$ 和 $\alpha_{\min}^m$，则第 $t$ 次迭代的学习率为
$$
\alpha_t=\alpha_{\min}^m + (\alpha_{\max}^m - \alpha_{\min}^m)\cdot \max(0, 1 - |\frac{t}{\Delta T} - 2m + 1|)
$$

• 带热重启的随机梯度下降： 该方法采用热重启方式来替代学习率衰减方法。每间隔一段时间，学习率会重新初始化为某个预设的值，之后继续衰减。

假设整个迭代过程共重启 $M$ 次，每次的重启周期为 $T_m$，重启后采用余弦衰减方法来降低学习率。则 $t$ 次迭代后的学习率为
$$
\alpha_t=\alpha_{\min}^m + \frac{1}{2}(\alpha_{\max}^m - \alpha_{\min}^m)(1 + \cos(\frac{T_{cur}}{T_m} \pi))
$$

其中，$\alpha_{\min}^m$ 和 $\alpha_{\min}^m$ 表示第 $m$ 个周期内，学习率的最大和最小值。$T_m$ 为重启周期，$T_{cur}$ 为上次重启之后的 epoch 数。

不管是哪种周期调整方式，尽管在某一段时间内，学习率会周期性上升或下降，但从全局来看，学习率整体仍保持着下降的趋势，这也为模型的收敛稳定性提供了保障。

在梯度下降法中，每次参数迭代的对象都涉及到多个参数。然而，对于每个参数，对应的学习率都完全相同。由于每个参数在对应维度上的收敛速度互不相同，则会导致某些参数对于更新方向不够敏感，从而造成精度损失。早期的一种在训练时适应模型参数各自学习率的启发式方法是，如果损失对于某个给定参数模型的偏导保持相同符号，则学习率增加，反之减小。这也是自适应学习率思想的早期雏形。

自适应学习率是一种适应于参数的动态学习率设置方法，该方法根据参数收敛的不同情况，分别设置对应的学习率。接下来介绍三种经典的自适应学习率算法 —— AdaGrad、RMSprop、AdaDelta。

4.5.1 AdaGrad

AdaGrad 算法[5]采用累计平方梯度来独立适应所有模型参数的学习率，其学习率设置与梯度历史平方值总和呈现反比关系。若该参数的损失偏导较大，则学习率衰减速度较快，若损失偏导较小，则学习率下降较慢。其目的是让参数在更为平缓的倾斜方向上取得更大的进步。

首先，在第 $t$ 次迭代时，我们需要计算每个参数梯度平方的累计值
$$
G_t=\sum_{ au=1}^{t} g_{ au} \odot g_{ au}
$$

其中，$\odot$ 为按元素乘积，$g_{ au} \in \mathbb{R}^{| heta|}$ 为第 $ au$ 次迭代时的梯度。则 AdaGrad 最终的参数更新为

$$
\begin{aligned}
heta_{t+1} &= heta_t + \Delta heta \\
&= heta_t - \frac{\alpha}{\sqrt{G_t + \epsilon}}\odot g_t
\end{aligned}
$$

尽管 AdaGrad 算法考虑到了不同参数的梯度变化情况，但是当经过一定迭代次数之后，若仍然未找到最优点，则由于学习率较小，会很难继续找到最优点。

4.5.2 RMSprop

AdaGrad 算法采用了历史累计平方梯度来适应参数学习率，这会使得学习率迅速衰减，因此。RMSprop[20]在此基础上进行了优化，采用指数衰减平均来丢弃遥远的历史。具体来说，它将梯度积累方法改变为指数加权的移动平均方法，使得过于遥远的梯度在调整学习率时的重要性降低。这样的改进，使得学习率并不完全呈现衰减趋势，可变小也可变大，避免了过早衰减的问题。

方法的整体迭代流程与 AdaGrad 类似，唯一不同的是将累计梯度平方改为了指数衰减移动平均。具体计算方法为

$$
\begin{aligned}
G_t &=\beta G_{t-1} + (1 - \beta) g_t \odot g_t \\
&=(1 - \beta) \sum_{ au=1}^t \beta^{t- au} g_{ au} \odot g_{ au}
\end{aligned}
$$

同样的，RMSprop 最终的参数更新为

$$
\begin{aligned}
heta_{t+1} &= heta_t + \Delta heta \\
&= heta_t - \frac{\alpha}{\sqrt{G_t + \epsilon}}\odot g_t
\end{aligned}
$$

其中，$\beta$ 为衰减率，一般设置为 0.9；$\alpha$ 为初始学习率，一般设置为 0.001。

4.5.3 AdaDelta

AdaDelta[22]在 RMSprop 的基础上做了进一步的改进。和 RMSprop 一样，在调整学习率时采用了指数衰减移动平均的方法。唯一不同的时，AdaDelta 在进行参数更新时，其参数更新差值 $\Delta heta$ 也采用了指数衰减平均的方式进行动态变化。

具体的，该方法将参数更新表达式中的初始学习率 $\alpha$ 替换为一个随时间变化的参数 $\sqrt{\Delta X^2_{t-1} + \epsilon}$，其中微小量 $\epsilon$ 用来保证数值稳定。则 $\Delta heta$ 的指数衰减移动平均计算方式为

$$
\Delta X^2_{t-1}=\beta_1 \Delta X^2_{t-2} + (1 - \beta_1)\Delta heta_{t-1} \odot \Delta heta_{t-1}
$$

其中 $\beta_1$ 为衰减率，最终的参数更新方式为
$$
\begin{aligned}
heta_{t+1} &= heta_t + \Delta heta \\
&= heta_t - \frac{\sqrt{\Delta^2_{t-1}} + \epsilon}{\sqrt{G_t + \epsilon}}\odot g_t
\end{aligned}
$$

在梯度下降法中，一个重要的前提条件是，函数在某一点的最速下降方向为该点的梯度反方向，因此采用梯度对参数进行迭代更新。然而，在小批量梯度下降中，由于样本选取的随机性，导致其梯度估计也存在一定的随机性，从而导致损失振荡下降，训练不够稳定。因此，需要设计一种新的梯度估计方法，让梯度的更新在训练过程中保持稳定，不受样本随机性的干扰。

若能降低单次训练中随机样本带来的梯度随机性，则能够有效缓解损失振荡的现象。一种较为直接的想法是，采用最近一段时间训练时的平均梯度来代替单次训练的梯度，从而使参数更新的方向更加稳定，提高整体的优化速度。

动量法[15]则是基于这样的思想，对梯度下降的更新方向进行了稳定，缓解了振荡现象，从而加速了优化速度。具体地，它将参数更新中的负梯度更新方向改为了负梯度的“加权移动平均”方向，使得每个参数的实际更新差值由最近一段时间内梯度的加权平均值决定。在第 $t$ 次迭代中，参数的更新公式为
$$
\begin{aligned}
heta_t &= heta_{t-1} + \Delta heta_t \\
&= heta_{t-1} + \rho \Delta heta_{t-1} - \alpha g_t \\
&= heta_{t-1} - \alpha \sum_{ au=1}^t \rho^{t- au} g_{ au}
\end{aligned}
$$

其中，$\rho$ 为动量衰减因子，通常设置为 0.9或近似值；$\alpha$ 为学习率。如图 4 所示，引入了累计加权平均梯度的动量方法后，振荡现象明显减弱，参数能够更快并更准确地向最优方向收敛。

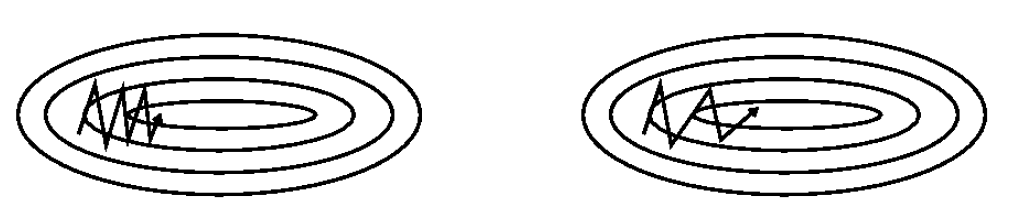
动量法实质上来自于一个物理类比。动量是质量和速度的乘积，我们规定单位质量，则动量大小即为速度大小，在迭代公式中即为 $\Delta heta$。我们将收敛过程抽象成一个小球从山顶向山谷滚去，在更新公式中，当前时刻的梯度值 $-\alpha g_t$ 即为力的提供者，推动小球沿着最为陡峭的方向向下滚动，从而累计动量，速度不断加快。另外，累计梯度 $\rho \Delta heta_{t-1}$ 代表了粘滞阻力，当小球遇到上坡或障碍时，该阻力的存在能够及时阻止其偏离方向，从而阻止其发生大幅度振荡，加速其滚动至最低点。

动量法中，单一梯度被修正为累计加权平均梯度，有效缓解了振荡现象的发生。然而，这样的方法仍然存在一定的问题。仍以小球滚动为例，动量法中，只有当小球开始产生振荡，偏离最速下降方向之后，它才会意识到错误，开始进行相应的调整。而更科学高效的方法应该是，在小球意识到将要偏离方向之前，就开始有意识地对自身的下降方向进行调整。它应当具备一定的预测判断能力。

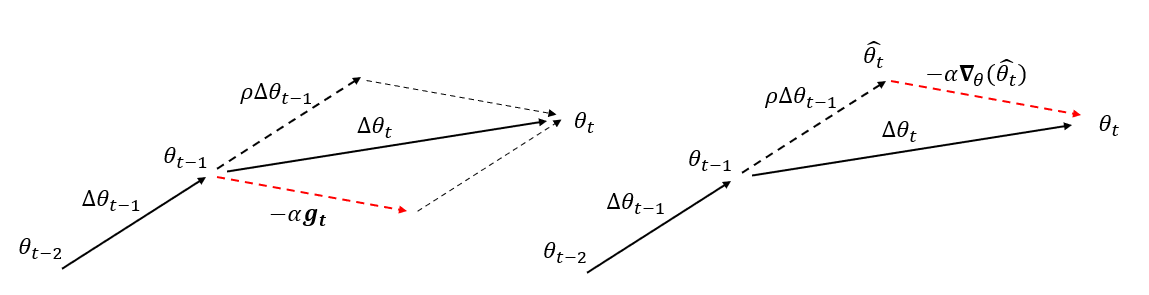
动量法中，我们首先计算了当前时候的负梯度值 $-g_t$，并与上一时刻的梯度更新方向 $\Delta heta_{t-1}$ 进行加权求和，获取当前时刻的梯度更新结果。而在 Nesterov 加速梯度动量[14]中，梯度计算的执行被安排在施加当前速度之后。具体的计算公式如下

$$
\begin{aligned}
heta_t &= heta_{t-1} + \Delta heta_t \\
&= heta_{t-1} + \rho \Delta heta_{t-1} - \alpha abla_{ heta}( heta_{t-1} + \rho \Delta heta_{t-1})
\end{aligned}
$$

Nesterov 动量可以解释为往标准动量方法中添加了一个校正因子。在动量法中，梯度更新方式可以被拆分为两步。首先，利用累计梯度校正参数，即 $\hat{ heta}t= heta{t-1} + \rho \Delta heta_{t-1}$，之后，再加入当前梯度值，进行梯度下降，即 $ heta_{t}=\hat{ heta}t - \alpha g_t$。然而，我们在首先对参数进行了校正后，仍然对当前时刻的梯度进行了计算，一种更合理的方式应该是，对校正后的参数进行梯度计算，能够进一步缓解当前梯度的随机性带来的误差。因此，将 $\alpha g_t$ 改为 $\alpha abla{ heta}( heta_{t-1} + \rho \Delta heta_{t-1})$，便得到了 Nesterov 动量的核心思想。该方法与原始动量方法的可视化比较如图 5 所示。

Adam 算法[10]是动量法和 RMSprop 的结合，它不但使用动量作为参数更新的方向，同时也可以自适应地调整学习率，帮助其稳定收敛。

第 $t$ 次迭代时，Adam 算法首先计算了累计梯度平方的加权平均 $G_t$ 和梯度加权平均 $M_t$，计算公式如下
$$
\begin{aligned}
&G_t=\beta_1 G_{t-1} + (1 - \beta_1) g_t \odot g_t \\
&M_t=\beta_2 M_{t-1} + (1 - \beta_2) g_t
\end{aligned}
$$

其中，$\beta_1$ 和 $\beta_2$ 分别为两个移动平均的衰减率，取值通常趋近于 1。在迭代初期，$G_t$ 和 $M_t$ 通常会比真实值更小，且偏差较大。因此需要对偏差进行修正
$$
\begin{aligned}
&\hat{G}_t=\frac{G_t}{1 - \beta^t_1} \\
&\hat{M}_t=\frac{M_t}{1 - \beta^t_2}
\end{aligned}
$$

修正后，可以得到 Adam 算法的最终更新公式
$$
heta_{t}= heta_{t-1} - \frac{\alpha}{\sqrt{\hat{G}_t} + \epsilon} \hat{M}_t
\label{Adam}
$$

一般来说，$\beta_1$ 取0.999，$\beta_2$ 取0.9，$\epsilon$ 为稳定数值的微小量，一般取 $10^{-8}$。与其他算法相比，Adam 算法在实际应用中表现更为突出。

Nadam[4]算法在 Adam 算法的基础上，进一步引入了 Nesterov 加速梯度。在公式\ref{Adam} 中，梯度估计值 $\hat{M}_t$ 是利用动量法进行更新的（参考公式\ref{21} 和~\ref{22}）。Nadam 对梯度估计值进行了调整。修正后的迭代公式为
$$
\begin{aligned}
heta_{t} &= heta_{t-1} - \frac{\alpha}{\sqrt{\hat{G}_t} + \epsilon} \hat{M}t \\
&= heta{t-1} - \frac{\alpha}{\sqrt{\hat{G}t} + \epsilon} (\frac{\beta_1 M{t-1}}{1 - \beta_1^t} + \frac{(1 - \beta_1)g_t}{1 - \beta_1^t})
\end{aligned}
$$

在深层次网络中，由于网络层数过深，在进行梯度的反向传播链式法则计算时，很有可能由于某一层梯度的过小或过大，造成累乘的放大效应，导致梯度消失或梯度爆炸现象的出现。例如，若权重初始化值较小，在各层上相乘得到的数值均在0-1之间，而激活函数梯度也在0-1之间，则连乘后数值会变得非常小，导致梯度消失。权重初始化较大同理。同样的，不合适的激活函数也会导致同样的效果。例如 sigmoid 函数。

在梯度计算时，最简单的避免梯度消失或梯度爆炸的方式是梯度截断。其思想也很简单，即把梯度限定在一个区间，当梯度的模小于或大于这个区间时就进行截断。一般有按值截断和按模截断两种方式。按值截断即限制了梯度向量中每个元素的取值。若某个参数的梯度小于或大于某个预设的阈值，则将该梯度固定为该阈值。按模截断限制了梯度向量的模长，假设截断阈值为 $ au$，若 $||g_t|| < au$，则保持 $||g_t||$ 不变；若 $||g_t|| > au$，则 $g_t=\frac{b}{||g_t||} g_t$。

由于深度学习优化问题本身的复杂性，仅仅对优化算法本身进行改进还不足以保证整个问题的完善求解。更多时候，一些外部因素往往会成为优化算法成功执行的制约条件。本部分将从参数初始化和输入值预处理出发，简要介绍如何对优化算法之外的一些关键要素进行优化，从而辅助优化算法在深度学习问题上更好地执行。

深度学习模型的优化算法是迭代算法，因此要求指定一些开始迭代的初始点。训练深度模型是一个困难的问题，大多数优化算法都很大程度地受到初始化选择的影响。初始点能够决定算法是否收敛，有些初始点不稳定，使得该算法会遭遇数值困难。当学习收敛时，初始点可以决定学习收敛得多快，以及是否收敛到一个代价高或低的点。

现代的参数初始化策略大多为启发式的，该问题事实上仍然没有被很好地解决。比较常用的初始化方法有这样几种：（1）预训练初始化。预训练模型的一大初衷，就是帮助下游任务获得一套更优的初始化参数，加速下游任务的收敛，提高泛化能力。例如经典的BERT[8]、Roberta[11]等模型，至今仍被广泛沿用，尤其是自然语言处理任务。将预训练模型应用在下游任务上的过程被称为微调。（2）随机初始化。随机初始化的一大目的，是为了破坏“对称权重”现象。如果具有相同激
活函数的两个隐藏单元连接到相同的输入，且这些单元具有相同的初始参数，那么优化算法将一直以相同的方式更新这两个单元。因此，随机化权重可以确保没有输入模式丢失在前向传播的零空间中，没有梯度模式丢失在反向传播的零空间中，使得不同神经元之间的区分性更好。（3）固定值初始化。对于一些特殊的参数，我们可以根据经验用一个特殊的固定值来进行初始化．比如偏置通常用0 来初始化，但是有时可以设置某些经验值以提高优化效率。

总体来说，随机初始化通常更能够显著改善优化问题的结果。对于预训练初始化，尽管具有更好的收敛性和泛化性，但是灵活性不够，不能在目标任务上任意地调整网络结构。而固定值初始化过于依赖于经验，很多时候显然不具有说服力。因此，好的初始化方法对于优化问题依然十分重要。

比较简单的随机初始化方法固定了初始权重的方差，采用经典分布对初始值进行采样。例如高斯分布初始化，参数满足$ heta \sim \mathcal{N}(0, \sigma^2)$。或者采用均匀分布初始化，参数 $ heta$ 在给定区间 $[-r, r]$ 之间选择。若满足方差为 $\sigma^2$，则 $r=\sqrt{3 \sigma^2}$。不管采用何种分布，方差的设置都十分关键。若方差过小，则神经元输出过小，经过多层网络后会逐渐消失；若方差过大，则激活函数容易过饱和，尤其是对于sigmoid类型的函数而言，容易导致梯度消失。

一种更加有效的随机初始化方式，是根据神经元的连接数量来自适应地调整初始化分布的方差，尽可能保持每个神经元的输入和输出的方差一致。较为典型的是 Glorot and Bengio 提出的标准初始化方法[6]，对于 $m$ 个输入和 $n$ 个输出的全连接层，其初始化参数分布为

$$
heta \sim U(-\sqrt{\frac{6}{m+n}}, \sqrt{\frac{6}{m+n}})
$$

上面介绍的两种基于方差的初始化方法都是对权重矩阵中的每个参数进行独立采样．由于采样的随机性，采样出来的权重矩阵依然可能存在梯度消失或梯度爆炸问题。为了避免这样的问题出现，我们希望误差项在反向传播中具有范数保持性。具体的，假设一个 $L$ 层的等宽线性网络，前向传播过程为 $y=W^{(L)} W^{(L-1)} \dots W^{(1)} x$，其中 $W^{(l)} \in \mathbb{R}^{M imes M}$ 为第 $l$ 层权重矩阵。范数保持性即，对于反向传播中每一层的误差项 $\delta^{(l-1)}=(W^{(l)})^T \delta^{(l)}$，均有 $||\delta^{(l-1)}||^2=||\delta^{(l)}||^2=||(W^{(l)})^T \delta^{(l)}||^2$。从这点出发，只需要将 $W^{(l)}$ 初始化为正交矩阵即可。这种方法称为正交初始化。

除了参数初始化比较困难之外，不同输入特征的尺度差异比较大时，梯度下降法的效率也会受到影响。尺度不同会造成在大多数位置上的梯度方向并不是最优的搜索方向，当使用梯度下降法寻求最优解时，会导致需要很多次迭代才能收敛。如果把数据归一化为相同尺度，则大部分位置的梯度方向近似于最优搜索方向．这样，在梯度下降求解时，每一步梯度的方向都基本指向最小值，训练效率会大大提高。对于尺度敏感的模型，必须先对样本进行预处理，将各个维度的特征转换到相同的取值区间，并且消除不同特征之间的相关性，才能获得比较理想的结果。

假设有 $N$ 个输入样本 ${x^{(n)}}_{i=1}^N$，有如下几种归一化方法：

• 最值归一化：该方法通过将每个输入特征的取值范围归一到 $[0, 1]$ 之间。具体的，对于每一维特征，归一化后的特征为
  $$
  \hat{x}^{(n)}=\frac{x^{(n)} - \min_n (x^{(n)})}{\max_n (x^{(n)}) - \min_n (x^{(n)})}
  $$
• 标准化：该方向将输入特征调整为均值为0，方差为1的标准正态分布。首先计算原分布的均值和方差

$$
\begin{aligned}
& \mu=\frac{1}{N} \sum_{n=1}^N x^{(n)} \\
& \sigma^2=\frac{1}{N} \sum_{n=1}^N (x^{(n)} - \mu)^2
\end{aligned}
$$

$$
\hat{x}^{(n)}=\frac{x^{(n)} - \mu}{\sigma}
$$

• 白化：白化是一种重要的预处理方法，用来降低输入数据特征之间的冗余性。输入数据经过白化处理后，特征之间相关性较低，并且所有特征具有相同的方差。白化的一个主要实现方式是使用主成分分析方法[21]去除掉各个成分之间的相关性。

本文针对优化算法应用在深度学习问题中的若干挑战，对优化算法进行了归类总结。我们首先介绍了基础的梯度下降法和牛顿法，并以梯度下降法为理论基础进行算法改进。我们以批量大小为衡量标准，对优化问题的速度和精度进行了权重。之后，从学习率和梯度估计方法这两个角度出发，介绍了若干针对性的改进方法。最后，跳出优化算法本身，对模型初始化参数和输入值尺度进行了简单的探讨。实际上，优化问题仍然还存在许多可以改进的算法点，例如，牛顿法可以引申出拟牛顿法、共轭梯度法等更加高效的二阶方法，这些方法将在后续工作中继续探讨。

[1] Dimitri P Bertsekas. Nonlinear programming. Journal of the Operational Research Society, 48(3):334–334, 1997.
[2] Léon Bottou, Frank E Curtis, and Jorge Nocedal. Optimization methods for large-scale machine learning. Siam Review, 60(2):223–311, 2018.
[3] John E Dennis Jr and Robert B Schnabel. Numerical methods for unconstrained optimization and nonlinear equations. SIAM, 1996
[4] Timothy Dozat. Incorporating nesterov momentum into adam. 2016.
[5] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research, 12(7), 2011.
[6] Xavier Glorot and Yoshua Bengio. Understanding the di?iculty of training deep feedforward neural networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pages 249–256. JMLR Workshop and Conference Proceedings, 2010.
[7] Akhilesh Gotmare, Nitish Shirish Keskar, Caiming Xiong, and Richard Socher. A closer look at deep learning heuristics: Learning rate restarts, warmup and distillation. arXiv preprint arXiv:1810.13243, 2018.
[8] Kenton L. Kristina T. Jacob D., Chang M. W. BERT: pre-training of deep bidirectional transformers for language understanding. In proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT), pages 4171–4186, 2019.
[9] Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy, and Ping Tak Peter Tang. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv preprint arXiv:1609.04836, 2016.
[10] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
[11] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692, 2019.
[12] Ilya Loshchilov and Frank Hutter. Sgdr: Stochastic gradient descent with warm restarts. arXiv preprint arXiv:1608.03983, 2016.
[13] Olvi L Mangasarian. Nonlinear programming. SIAM, 1994.
[14] Yurii Nesterov. A method for unconstrained convex minimization problem with the rate of convergence o(1/$k^2$). In Doklady an ussr, volume 269, pages 543–547, 1983.
[15] Ning Qian. On the momentum term in gradient descent learning algorithms. Neural networks, 12(1):145–151, 1999.
[16] Herbert Robbins and Sutton Monro. A stochastic approximation method. The annals of mathematical statistics, pages 400–407, 1951.
[17] Sebastian Ruder. An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747, 2016.
[18] Leslie N Smith. Cyclical learning rates for training neural networks. In 2017 IEEE winter conference on applications of computer vision (WACV), pages 464–472. IEEE, 2017.
[19] Suvrit Sra, Sebastian Nowozin, and Stephen J Wright. Optimization for machine learning. Mit Press, 2012.
[20] Tijmen Tieleman, Geoffrey Hinton, et al. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural networks for machine learning, 4(2):26–31, 2012.
[21] Svante Wold, Kim Esbensen, and Paul Geladi. Principal component analysis. Chemometrics and intelligent laboratory systems, 2(1-3):37–52, 1987.
[22] Matthew D Zeiler. Adadelta: an adaptive learning rate method. arXiv preprint arXiv:1212.5701, 2012.